Profit/Loss decomposition
Consider the acquisition at time $t_0$ of one unit of a stock offered in currency $C_1$, using a base/home currency $C_2$. The price in the base currency, excluding fees, is $$E_{12}(t_0)P(t_0),$$ where:
- $E_{12}$ is the exchange rate from $C_1$ to $C_2$;
- $P$ is the unit price of stock, in currency $C_1$.
Later, at time $t$, the unrealized profit or loss (PL) in the base currency $C_2$ is equal to $$\text{PL}=E_{12}(t)P(t) - E_{12}(t_0)P(t_0),$$ which can be decomposed as $$\text{PL}=E_{12}(t)\big(P(t)-P(t_0)\big) + \big (E_{12}(t) - E_{12}(t_0)\big) P(t_0)=\text{Product PL} + \text{Currency PL},$$ where:
- The first term (Product PL, in base currency) corresponds to the product profit/loss in the product currency $C_1$ converted in the home currency $C_2$ with the current exchange rate.
- The second term (Currency PL) corresponds to the change in exchange rate multiplied by the initial value. It will decrease (resp. increase) the total profit/loss $\text{PL}$ if the base currency strengthens (resp. weakens). This corrects the product PL estimate, which assumes that the acquisition is done at the current exchange rate, while it might have been more or less expensive.
In particular, the total PL will generally be larger or smaller than the product PL, due to the currency PL.
In other words:
The naive idea of computing PL in the stock currency and converting it to the base currency using the current exchange rate is generally incorrect.
Multiple buys
When stock is acquired at times $t_1,\dots,t_N$, the above formula generalizes to
$$ \begin{aligned} \text{PL} &= \left(E_{12}(t)NP(t) - \sum_{i=1}^N E_{12}(t_i)P(t_i)\right) \newline &= E_{12}(t)N\left(P(t) - \frac{1}{N}\sum_{i=1}^N P(t_i)\right) + \sum_{i=1}^N \big(E_{12}(t) - E_{12}(t_i)\big) P(t_i) \end{aligned} $$
The first term is simply the product PL in the base currency with respect to the average acquisition cost (or break-even price) $1/N\sum_{i=1}^N P(t_i)$.
Product PL or Product+Currency PL?
The fact that converting the product PL to the base currency is not equal to the total PL can be a source of confusion and bugs in portfolio tracking tools, as well as in the brokers’ own interfaces.
- The Interactive Brokers mobile or web app mainly displays the product PL, while currency PL is accounted for separately or only indirectly:
- The Unrealized P&L values in the Portfolio tab seems to only take into account the product PL, even though it is specified in the base currency.
- The “Display position in base currency” setting applies the exchange rate to positions’ unrealized PL, thus also only computes the product PL.
- When generating a report from the Statements tab, the Mark-to-Market Performance Summary table will contain the product PL (in the original currencies) in the Stock section and the aggregated currency PL in the Forex section, across stocks held in currencies different from the base currency. The PL in the Open Positions section is the product PL only, and the conversion to the base currency is performed by applying the current exchange rate.
- On the other hand, the PortfolioAnalyst Change in NAV section computes the total PL, as it simply looks at the current value in the base currency compared to the deposits and withdrawals.
- On the other hand, DEGIRO separately reports the Product and Currency PL. The documentation explains that the computation is based on the break-even price, matching the equation above. The Total PL in the account overview is indeed the combination of product and currency PL.
- The open source investment tracking projects Wealthfolio and Ghostfolio both have open issues regarding the product PL only being computed, which is misleading for end users: 1 2 3 4 5
For Wealthfolio, the issue can be fixed by replacing
// Cost basis in the account currency. final_cost_basis_acct += self.fx_service.convert_currency_for_date( position.total_cost_basis, position_currency, &account_currency, target_date)which corresponds to later computing $E_{12}(t)\sum_{i=1}^N(P(t) - P(t_i))$, i.e. the product PL, by
for lot in &position.lots { final_cost_basis_acct += self.fx_service.convert_currency_for_date( lot.cost_basis, // Stored in the position currency position_currency, &account_currency, lot.acquisition_date.naive_utc().date())?; }which computes the true acquisition cost $\sum_{i=1}^N E_{12}(t_i)P(t_i)$, later compared with the current value $E_{12}(t)NP(t)$.
Long-term behaviour of currency and product PLs
In the above decomposition of the total PL as product and currency PL:
- the currency PL, $(E_{12}(t)-E_{12}(t_0))P(t_0)$, is only a function of the acquisition price and the difference in exchange rates, while
- the product PL, $E_{12}(t)(P(t)-P(t_0))$, depends on the stock price appreciation and the current exchange rate.
When considering currency pairs where the exchange rate is roughly stationary (many major currencies pairs over a long time) and market indices, it can therefore be expected that:
On the long term, the currency PL becomes a secondary factor of the total PL:
Indeed, this reflects the fact that exchange rates are relative prices and stay roughly constant, while stock prices grow through compounding.
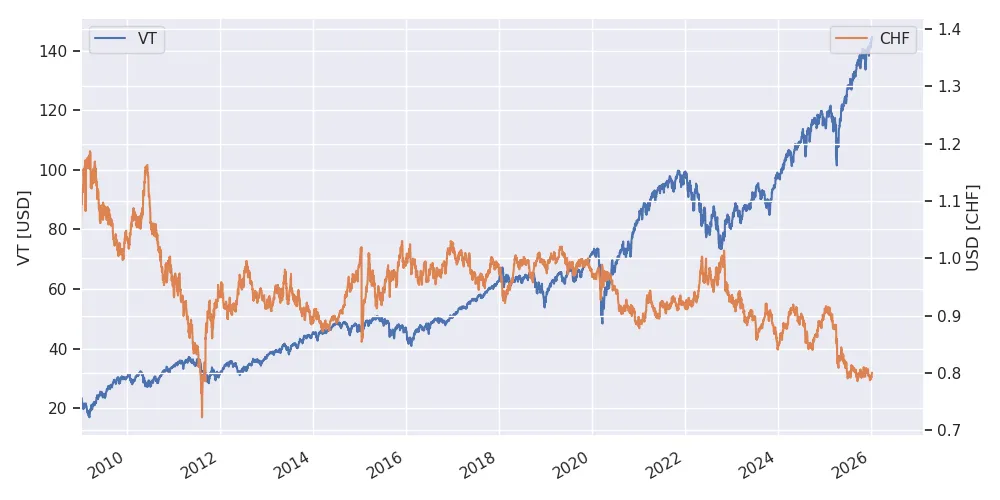
Example: VT ETF in CHF
Consider the VT ETF with $C_1=\text{USD}$ and $C_2=\text{CHF}$. The monthly prices since 2009 are illustrated below. The CHF strengthens against the USD (i.e. $E_{12}$ decreases) episodically, and the ETF rises in value.
When computing the total PL and the two components with the expression above, we indeed see that the currency PL corrects down the product PL value.
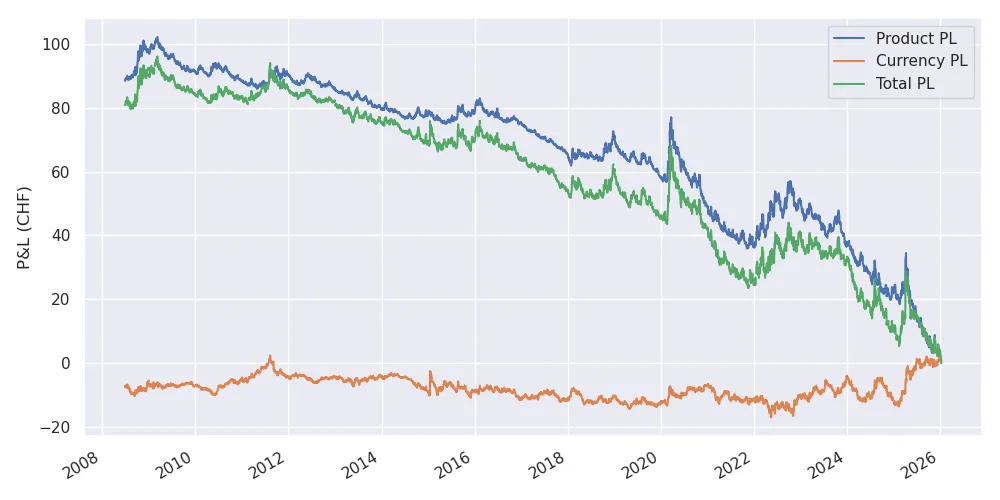
Product, Currency, and total PL on January 10, 2026, for the acquisition of one unit of VT stock in CHF at the given date in the past.
On the other hand, the size of the currency PL remains relatively small. The following plot shows its relative size compared to the product PL, in the setup of the previous plot.
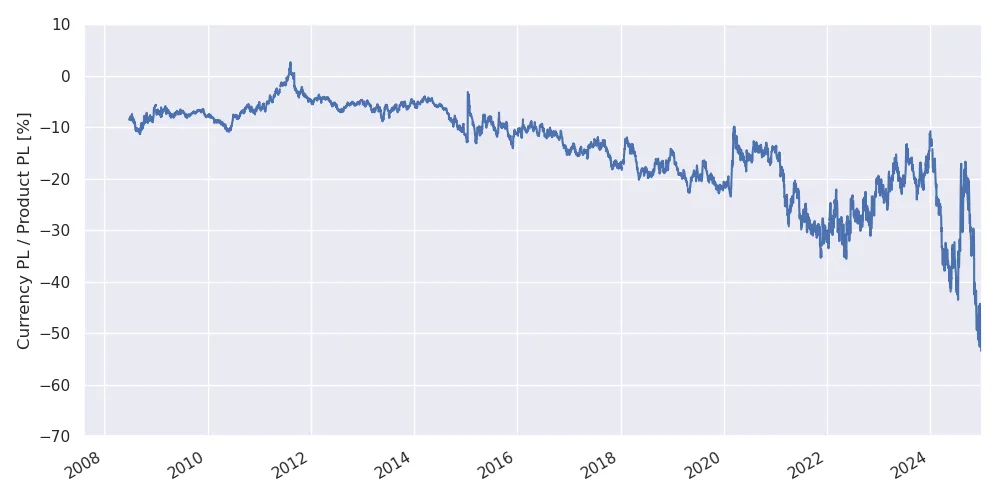
Relative size of the PL components.
While the currency effect can be quite important in the short term (e.g. up to 50% for a 2024 acquisition), for a buy date between 2008 and 2018, the currency PL is at most 20% of the product PL, matching with the arguments above.
Example: MSCI World ETF in CHF
Similarly, consider the HSBC MSCI World ETF in EUR:
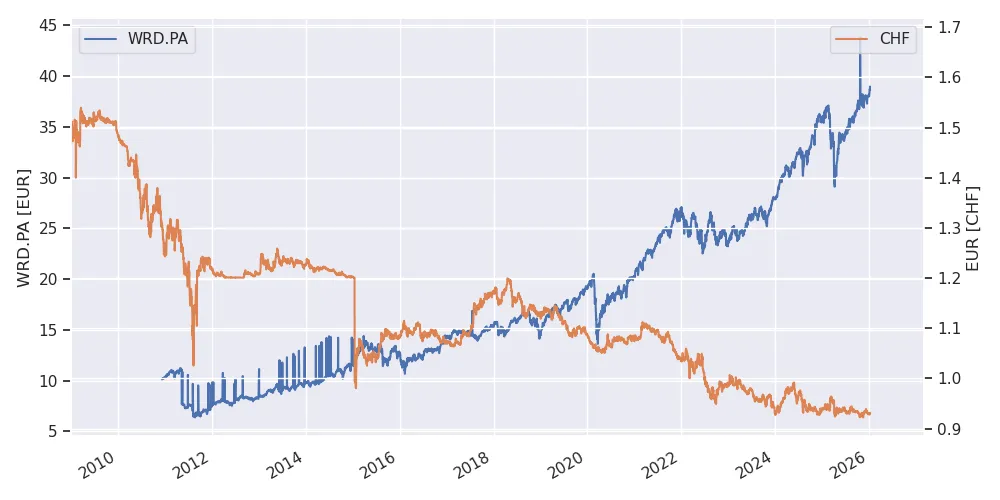
MSCI World price in EUR and the EURCHF price $E_{12}$. The CHF also becomes stronger with respect to the EUR. The fall of the exchange rate in 2015 corresponds to the discontinuation of the minimum exchange rate by the SNB. Source: Yahoo Finance.
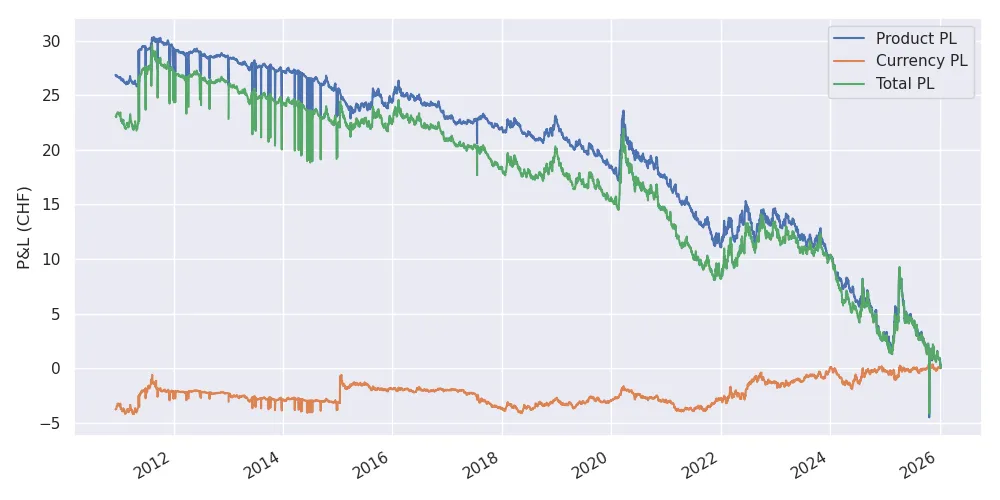
Product, Currency, and total PL on January 10, 2026, for the acquisition of one unit of WRD.PA stock in CHF at the given date in the past.
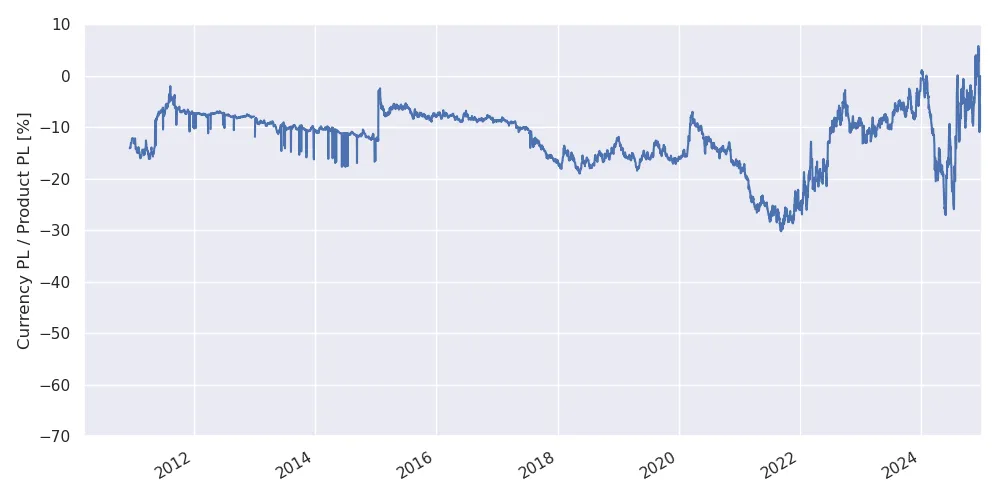
Relative size of the currency PL compared to the product PL. Similarly, for buy dates before 2020, the currency PL is at most 20% of the product PL.